Filled Julia set
The filled-in Julia set 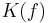 of a polynomial
of a polynomial 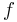 is a Julia set and its interior.
is a Julia set and its interior.
Contents |
Formal definition
The filled-in Julia set 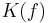 of a polynomial
of a polynomial 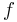 is defined as the set of all points
is defined as the set of all points 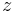 of dynamical plane that have bounded orbit with respect to
of dynamical plane that have bounded orbit with respect to 
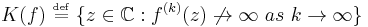
where :
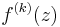 is the
is the 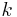 -fold composition of
-fold composition of 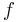 with itself = iteration of function
with itself = iteration of function 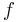
Relation to the Fatou set
The filled-in Julia set is the (absolute) complement of attractive basin of infinity.
Attractive basin of infinity is one of components of the Fatou set.
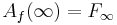
In other words, the filled-in Julia set is the complement of the unbounded Fatou component:
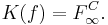
Relation between Julia, filled-in Julia set and attractive basin of infinity
Julia set is common boundary of filled-in Julia set and attractive basin of infinity
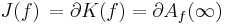
where :
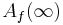 denotes attractive basin of infinity = exterior of filled-in Julia set = set of escaping points for
denotes attractive basin of infinity = exterior of filled-in Julia set = set of escaping points for 
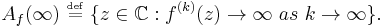
If the filled-in Julia set has no interior then Julia set coincides with filled-in Julia set. This happens when all the critical points of  are pre-periodic. Such critical points are often called Misiurewicz points.
are pre-periodic. Such critical points are often called Misiurewicz points.
Spine
The most studied polynomials are probably those of the form 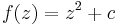 , which are often denoted by
, which are often denoted by 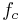 , where
, where  is any complex number. In this case, the spine
is any complex number. In this case, the spine 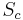 of the filled Julia set
of the filled Julia set 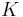 is defined as arc between
is defined as arc between 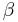 -fixed point and
-fixed point and 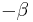 ,
,
![S_c = \left [ - \beta , \beta \right ]\,](/2012-wikipedia_en_all_nopic_01_2012/I/f4d5b48fdb364b0177f07b95236b0000.png)
with such properties:
- spine lies inside
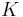 .[1] This makes sense when
.[1] This makes sense when 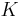 is connected and full [2]
is connected and full [2] - spine is invariant under 180 degree rotation,
- spine is a finite topological tree,
- Critical point
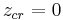 always belongs to the spine.[3]
always belongs to the spine.[3] 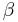 -fixed point is a landing point of external ray of angle zero
-fixed point is a landing point of external ray of angle zero 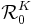 ,
,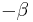 is landing point of external ray
is landing point of external ray 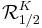 .
.
Algorithms for constructing the spine:
- detailed version is described by A. Douady[4]
- Simplified version of algorithm:
- connect
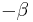 and
and 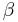 within
within 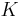 by an arc,
by an arc, - when
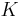 has empty interior then arc is unique,
has empty interior then arc is unique, - otherwise take the shortest way that contains
 .[5]
.[5]
- connect
Curve 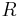 :
:

divides dynamical plane into two components.
Images
Notes
- ^ Douglas C. Ravenel : External angles in the Mandelbrot set: the work of Douady and Hubbard. University of Rochester
- ^ John Milnor : Pasting Together Julia Sets: A Worked Out Example of Mating. Experimental Mathematics Volume 13 (2004)
- ^ Saaed Zakeri: Biaccessiblility in quadratic Julia sets I: The locally-connected case
- ^ A. Douady, “Algorithms for computing angles in the Mandelbrot set,” in Chaotic Dynamics and Fractals, M. Barnsley and S. G. Demko, Eds., vol. 2 of Notes and Reports in Mathematics in Science and Engineering, pp. 155–168, Academic Press, Atlanta, Georgia, USA, 1986.
- ^ K M. Brucks, H Bruin : Topics from One-Dimensional Dynamics Series: London Mathematical Society Student Texts (No. 62) page 257
References
- Peitgen Heinz-Otto, Richter, P.H. : The beauty of fractals: Images of Complex Dynamical Systems. Springer-Verlag 1986. ISBN 978-0-387-15851-8.
- Bodil Branner : Holomorphic dynamical systems in the complex plane. Department of Mathematics Technical University of Denmark , MAT-Report no. 1996-42.
 is
is